Conjuntos Numéricos

· Conjunto dos Números Naturais (IN)

Um subconjunto importante de IN é o conjunto IN*:

IN*={1, 2, 3, 4, 5,...} ► o zero foi excluído do conjunto IN.

Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico abaixo:

· Conjunto dos números inteiros (Z)

O conjunto IN é subconjunto de Z.

Temos também outros subconjuntos de Z:

Z* = Z-{0}

Z₊ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,...}

Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,...}

Observe que Z₊ = IN.

Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:

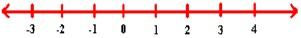
· Conjunto dos números racionais (Q)

Os números racionais são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador  Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.

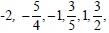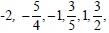Então:    por exemplo, são números racionais.

Exemplos:

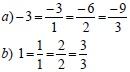
Assim, podemos escrever:

É interessante considerar a representação decimal de um número racional , que se obtém dividindo a por b.

Exemplos referentes às decimais exatas ou finitas.

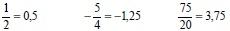
Exemplos referentes às decimais periódicas ou infinitas:

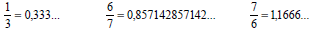
Toda decimal exata ou periódica pode ser representada na forma de número racional. 

· Conjunto dos números irracionais 

Os números irracionais são decimais infinitas não periódicas, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:

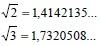
Um número irracional bastante conhecido é o número pi =3,1415926535...

· Conjunto dos números reais (IR)

Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o conjunto dos números reais como:

O diagrama abaixo mostra a relação entre os conjuntos numéricos:

Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:

IR* = IR-{0}

IR₊ = conjunto dos números reais não negativo

IR_ = conjunto dos números reais não positivos

Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:

- Entre os números 1 e 2 existem infinitos números reais:

1,01 ; 1,001 ; 1,0001 ;  1,1 ;  1,2  ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...

- Entre os números 5 e 6 existem infinitos números reais:

5,01 ; 5,02 ; 5,05 ;  5,1 ;  5,2  ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...