Cálculo Diferencial

Para os leitores mais interessados nas origens das palavras, calculus, na Roma antiga, era uma pequena pedra ou seixo utilizado para contagem e jogo, e o verbo latino calculare passou a significar "figurar", "computar", "calcular". Hoje o Cálculo é um sistema de métodos para resolver problemas quantitativos de uma natureza particular, como no cálculo de probabilidades, no cálculo de variações, etc. O cálculo abordado agora é às vezes chamado o Cálculo para distingui-lo de todos os outros cálculos subordinados.

Às vezes é dito que o cálculo foi inventado por aqueles dois grandes gênios do século XVII, Newton e Leibniz. Na verdade o Cálculo é produto de um longo processo evolutivo que começou na Grécia Antiga e continuou no século XIX. Newton e Leibniz foram homens verdadeiramente notáveis e suas contribuições foram de importância decisiva, mas o assunto nem começou tampouco terminou com eles.

Problemas semelhantes estavam presentes nas mentes de muitos cientistas europeus do século XVII, tendo destaques às realizações de Fermat, onde cada um colaborou imensurávelmente com engenhosos métodos de resolução de problemas. A grande realização de Newton e Leibniz foi reconhecer e explorar a intrínseca relação entre o problema da tangente a uma função f(x) e a área sob esse mesmo gráfico, que na época ninguém entendia muito bem.

Podemos dizer que eles foram os primeiros a entenderem profundamente o Teorema Fundamental do Cálculo, o que diz que a solução do problema da tangente pode ser utilizada para resolver o problema da área. Esse teorema, certamente o mais importante da matemática, foi descoberto por cada um deles, quase que simultaneamente, independentemente um do outro. Porém sendo o trabalho de Leibniz mais claro, atribuíram-lhe todos méritos. Seus sucessores uniram os dois fantásticos raciocínios para criar uma arte de resolução de problemas de poder e versatilidade impressionantes.

OS PROBLEMAS BÁSICOS DO CÁLCULO.

Os problemas do cálculo resumem-se em um numero de dois, são eles: o problema das retas tangentes e o problema das áreas sob uma curva. Iniciaremos nossa abordagem pelo problema das tangentes, pois para dissolvermos o problema das áreas é necessário, anteriormente, o domínio de artifícios geométricos e algébricos propostos pelas tangentes.

Temos então uma reta tangente a uma curva expressa por y = f(x), nosso estará concentrado em encontrar o coeficiente angular formado entre a reta tangente e a curva. Antes de prosseguirmos devemos ter total conhecimento do que é uma reta tangente. Temos uma circunferência como exemplo, uma reta tangente seria aquela que interceptaria a circunferência em apenas um ponto, esse seria o nosso ponto de tangencia, portanto as retas não tangentes interceptam a curva em dois ou mais pontos ou interceptam-na em ponto nenhum.

Essa situação reflete a idéia que a maioria das pessoas tem de tangente à uma curva num ponto dado como sendo uma reta que toca a curva naquele ponto. Essa definição foi usada com sucesso pelos gregos ao tratarem de circunferências e algumas curvas especiais, mas, para curvas em geral, ela é falha.

Eis que Fermat, grande matemático do século XVII, generalizou o conceito de reta tangente à curvas quaisquer, o enunciado era o seguinte: considere uma curva f(x) e P um dado ponto fixo sobre essa curva. Considere Q um segundo ponto próximo de P sobre essa curva e desenhe uma reta secante PQ.

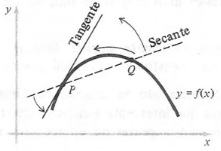
A reta tangente à P pode ser encarada como posição-limite da reta secante variável quando Q desliza ao longo da curva em direção a P. Essa idéia qualitativa nos leva a métodos quantitativos para o cálculo do coeficiente angular exato em termos da função f(x). É preciso não banalizar tal conceito, pois, sem ele, não haveria a formalização do conceito de velocidade e aceleração instantânea ou qualquer tipo de força em Física.